分数を約分を自動でしてくれるツールです。
約分計算機の使い方
使い方は以下のとおりです。
約分したい分数の分子(上の数字)と分母(下の数字)をそれぞれの入力欄に入力します。
分子と分母の入力が完了したら、「計算」ボタンをクリックまたはタップします。
黄色背景の欄に計算結果が表示されますので確認してください。
約分のやり方
約分は分数をできるだけ簡単な形にすることです。
分数を約分することで分子と分母の数が共通の約数で割り切れるようにします。
以下に、約分の基本的な方法を説明します。
約分の手順
分数の分子(上の数字)と分母(下の数字)の両方を割り切れる数を探します。これを「公約数」と呼びます。
分子と分母の最大公約数(GCD)を見つけ、それで両方を割ります。最大公約数は、分子と分母の共通の約数の中で最も大きな数です。
最大公約数で分子と分母をそれぞれ割り、分数を簡単な形にします。
約分の例

$\frac {12}{16}$こちらを約分するとします。
12と16の最大公約数は4です。
分子と分母を4で割ると$\frac {3}{4}$という答えになります。
約分の豆知識
約分に関する豆知識をいくつか紹介します。
素因数分解で素早く約分できる
約分の効率的な方法は素因数分解を使うことです。
分子と分母をそれぞれ素因数分解し、共通の因数を探して約分することで簡単な分数に変えられます。
例えば、30/45はそれぞれを素因数分解すると30 = 2 × 3 × 5、45 = 3 × 3 × 5となり、共通因数である3と5で約分し最終的に2/3になります。
「ユークリッドの互除法」で最大公約数を使う約分
約分をする際は「ユークリッドの互除法」を使う方法もあります。
大きな数の分数の約分に特に役立ちます。
例:$\frac {48}{18}$の場合は以下のような式になり、最大公約数は6となります。
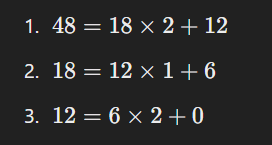
48÷18=2余り12を数式に入れると一番のような式になります。
古代バビロニアやエジプトでも分数の簡略化をしていた
古代文明でも分数をできるだけ簡単な形にすることが重要視されていました。
特にエジプトでは「単位分数」と呼ばれる、分子が1の分数(例:1/2、1/3)を使うことが基本で、複雑な分数は一連の単位分数に分割されました。
これは一種の「約分」の原理に基づくもので、分数を簡略化することが計算の基礎として重要だったことを示しています。
約分をあえてしない時代があった
現代では、分数を約分することが一般的ですが歴史的にはそうではない場合もありました。
例えば、16世紀の数学者たちは商業計算での便宜上約分をしないまま使うことが多かったそうです。
これにより、計算の途中で分母や分子を使いやすい数に保つことができたためです。
整数と分数の間で約分が可能
約分は分数の中だけでなく、整数と分数の間でも使われます。
例えば、$\frac{4}{2}$のように分子が分母の倍数である場合、分数を整数として表すことができます。
約分関連のよくある質問
- 約分計算機は通分にも使えますか?
-
はい、約分計算機を使って通分も可能です。分母が異なる分数を入力すると、最小公倍数を用いて分母を揃えた形で計算結果を表示してくれます。これにより、約分と通分を一度に確認できる便利なツールです。
- 分数の約分のルールについて教えてください
-
分数の約分の基本ルールは、分子と分母に共通する因数(共通の数)で割ることです。最も大きな共通因数で割ることで、分数を最も簡単な形にできます。例えば、2/4は2で割ると1/2になります。これが約分の基本的なルールです。
- 約分のやり方がわかりません。どうすればいいですか?
-
約分のやり方は簡単です。まず分子と分母に共通する数(共通因数)を見つけ、その数で両方を割ります。最大の共通因数で割ると、最も簡単な形の分数が得られます。
コメント