この計算機は分数の通分をしてくれます。
目次
通分の計算機の使い方と使用例
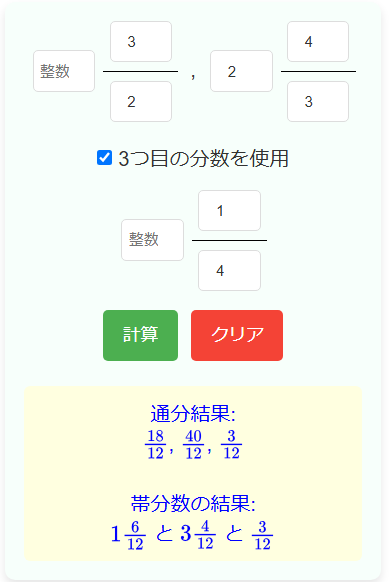
通分の計算機の使い方
- 3つ目の分数を使用する場合は「3つ目の分数を使用」にチェックを入れ、2つの分数で通分する場合はチェックを外します。
- 通分した分数の値を入力します。(整数は無しでも使えます)
- 計算ボタンを押すと通分された結果が黄色背景に表示されます。
通分について解説
通分とは異なる分母を持つ複数の分数を同じ分母にそろえることです。
通分をすると、分数同士の加減計算(足し算や引き算)がしやすくなります。
通分をする目的とは?
分数の足し算や引き算をする際、異なる分母を持つ分数同士を直接計算することはできないです。
通分をすると分数の分母がそれぞれそろい、後は分子の足し算や引き算をすると答えが求められます。
通分の手順を解説
通分の基本的な流れは以下の通りです。
①分母の最小公倍数を求める
まず、足し算・引き算を行いたい分数の分母同士の最小公倍数(両方の分母で割り切れる最小の数)を求めます。
② 分子と分母を同じ数でかける
次に各分数の分母を最小公倍数した数になるようかけ算して、分母にかけた数を分子にもかけます。
③他の分数も最小公倍数の数字に分母を合わせる
計算する分数全ての分母を合わせます。
通分の例
例1: $\frac{1}{3}$と$\frac{1}{4}$を通分する
- 分母の最小公倍数を求めます。3と4の最小公倍数は12です。
- それぞれの分数を、新しい分母にするために、分子と分母を掛けます。
- $\frac{1}{3}$の分母を12にするには、分母を4倍する必要があります。分子にも4を掛けます。
- $\frac{1}{3}=\frac{4}{12}$
- $\frac{1}{4}$の分母を12にするには、分母を3倍する必要があります。分子にも3を掛けます。
- $\frac{1}{4}=\frac{3}{12}$
- $\frac{1}{3}$の分母を12にするには、分母を4倍する必要があります。分子にも4を掛けます。
- これで分母が同じになりました:
- $\frac{4}{12}$と$\frac{3}{12}$
例2: $\frac{5}{6}$と$\frac{7}{8}$を通分する
- 分母の最小公倍数は、6と8の最小公倍数である24です。
- 各分数の分母24にそろえます。
- $\frac{5}{6}$の分母を24にするには、分母を4倍します。分子にも4を掛けます。
- $\frac{5}{6}=\frac{20}{24}$
- $\frac{7}{8}$の分母を24にするには、分母を3倍します。分子にも3を掛けます。
- $\frac{7}{8}=\frac{21}{24}$
- $\frac{5}{6}$の分母を24にするには、分母を4倍します。分子にも4を掛けます。
- 結果:
- $\frac{20}{24}$と$\frac{21}{24}$
これで、分母が24で揃ったので、あとは足し算や引き算が簡単に行えます。
4. 最小公倍数が見つからない場合
最小公倍数がすぐに見つからないときは、分母同士を掛けた数を新しい分母として使うこともできます。この方法は必ずしも最小ではない場合がありますが、通分が可能です。
例: $\frac{1}{5}$と$\frac{2}{7}$を通分する
- 分母を掛けて新しい分母を求めます。
- 5と7を掛けると35です。
- 各分数を35にそろえます。
- $\frac{1}{5}$の分母を35にするには7を掛けます。分子にも7を掛けます。
- $\frac{1}{5}=\frac{7}{35}$
- $\frac{2}{7}$の分母を35にするには、5を掛けます。分子にも5を掛けます。
- $\frac{2}{7} = \frac{10}{35}$
- $\frac{1}{5}$の分母を35にするには7を掛けます。分子にも7を掛けます。
- 結果:
- $\frac{7}{35}$と$\frac{10}{35}$
通分のよくある質問
- 通分とは何ですか?
-
通分とは複数ある分数の分母をそろえることです。複数の分数を足し算や引き算する時、分母が異なるとそのまま計算できないので、共通の分母(公分母)を見つけてそろえます。
- 通分はどんなときに使いますか?
-
分数同士の足し算や引き算をする場合に使います。
- 通分の手順は何ですか?
-
- 各分数の分母の最小公倍数を求めます。
- 各分数の分母そろえるため、分子と分母を同じ数で掛け算します。
- 分母がそろったら、分数の足し算や引き算を行います。
- 通分する際、分母の最小公倍数が分からないときはどうしますか?
-
分母を単純に掛け算して共通の分母を作る方法があります。
- 通分と約分の違いは何ですか?
-
通分は複数ある分数の分母をそろえることです。約分は分子と分母を同じ数で割って簡単な形にすることです。
コメント